SICP Chapter 2

Building Abstractions with Data

Data Abstraction

Isolate two parts of a program

1. Parts deal with how data objects are represented
2. Parts deal with how data objects are used

Selectors, Constructors

Interface between programs and data definition.

selector

select data attributes

constructor

construct data objects

list-structured data

Data objects constructed from Pair (compound-data primitive)

Abstraction Barriers

• use and only allow a basic set of operations to manipulate the data
• each layer uses procedures exposed by underlying layers (interface procedures)
• make programs much easier to maintain and to modify

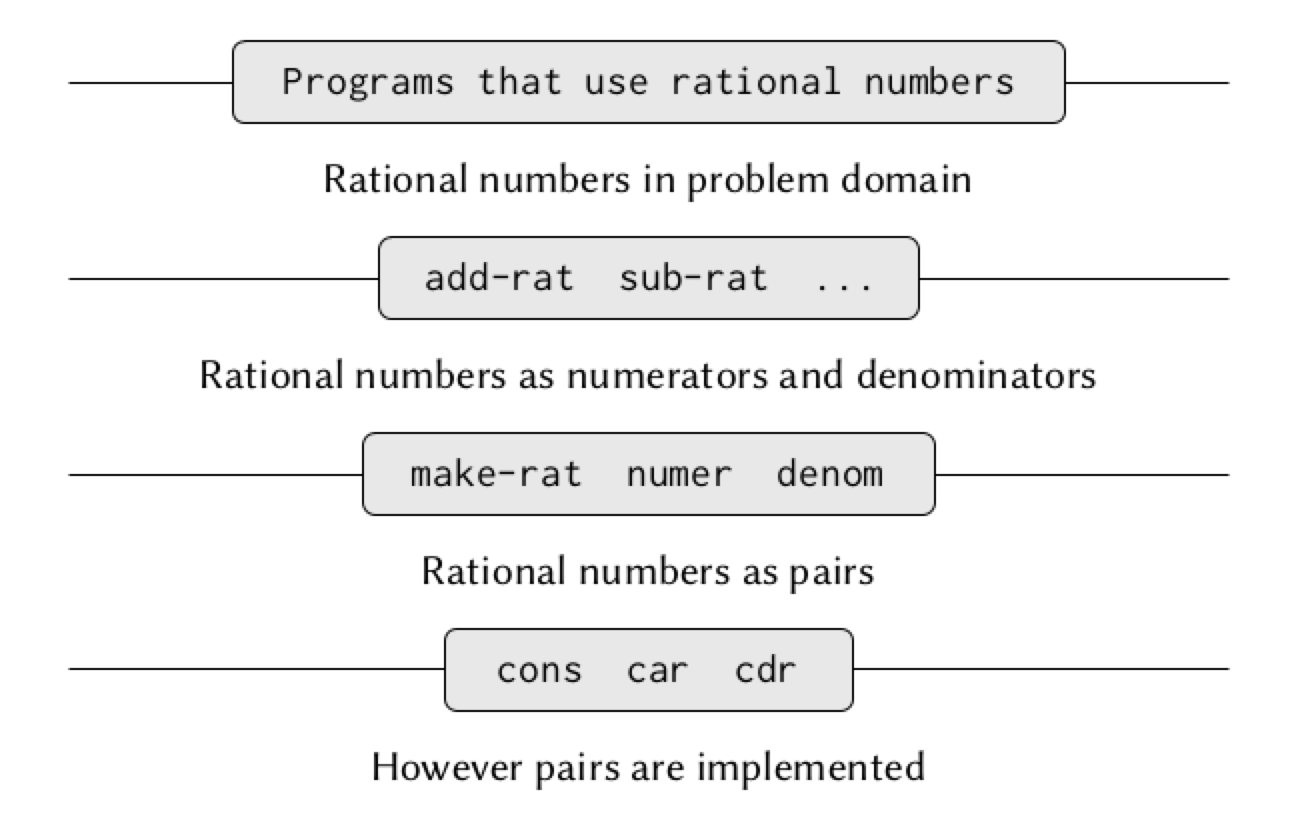
Example: Arithmetic Operations fro Rational Numbers

(define (make-rat n d)
  (let ((g ((if (< d 0) - +) (gcd n d))))
    (cons (/ n g) (/ d g))))

(define (numer x) (car x))
(define (denom x) (cdr x))

(define (add-rat x y)
  (make-rat (+ (* (numer x) (denom y))
               (* (numer y) (denom x)))
            (* (denom x) (denom y))))

(define (print-rat x)
  (newline)
  (display (numer x))
  (display "/")
  (display (denom x)))

Exercises

• Exercise 2.2 - Represent segments in planes
• Exercise 2.3 - Segments to Rectangles

What is data

• procedures (selectors and constuctors) plus conditions (procedures must fulfill to be a valid representation)
  • -> procedures/implementations can have many forms, as long as they comply with the conditions
• define new kinds of data objects in terms of previously defined types of data objects

Rational Number Example:

1. Procedures must meet the requirement below

     (numer x)    n
     --------- = ---
     (denom x)    d
   

2. Condition above rely on representation of integer

Exercises

• Exercise 2.4 - Alternative Implementation of Cons, Car, Cdr use Applicative order

• Exercise 2.5 - Represent non-negative int using only number and arithmetic operations

• Exercise 2.6 - Define numbers and addition without numbers Church Numeral

• Exercise 2.14~2.16 - Identity of Intervals

Hierarchical Data and the Closure Property

Closure Property of Cons

• create pairs whose elements are pairs
• an operation for combining data objects satisfies the closure property if the results of combining things with that operation can be combined using the same operation
• allows to create hierarchical structure - parts made up of parts

Sequences

• List

  • a sequence of pairs, formed by nested cons
  • (list 1 2 3 4) equals to (cons 1 (cons 2 (cons 3 (cons 4 nil))))

  • access an element

    (define (list-ref items n)
      (if (= n 0)
          (car items)
          (list-ref (cdr items) (- n 1))))
    (define squares (list 1 4 9 16 25))
    (list-ref squares 3)
    16
    

  • get a list’s length

    (define (length items)
      (define (length-iter a count)
        (if (null? a)
            count
            (length-iter (cdr a) (+ 1 count))))
      (length-iter items 0))
    

  • append

    (define (append list1 list2)
      (if (null? list1)
          list2
          (cons (car list1) (append (cdr list1) list2))))